クラスター分析（階層型分類法の基本事項）

クラスター分析は異なる性質が混ざった多数の個体を、個体間の類似度に基づいて似たものの集まり（クラスター）を作るための手法。判別分析ではどの群に属するかがあらかじめわかっているデータに基づいて判別関数（判別方法）を構成したのに対し、クラスター分析では分類のための外的な基準は与えられていない*1。クラスター分析は、階層型分析法と非階層型分類法に大別できる。階層型分類法は、最も似ている組み合わせから順番にクラスターを形成する。途中過程が階層のように表せるため、アウトプットとして樹形図（デンドログラム）を描くことができる。一方、非階層分類法は階層的な構造を持たない。あらかじめクラスターの数を決め、決めた数にデータを分割する方法。

個体間の類似度
クラスター間の距離
- クラスターの形成プロセス
- ウォード法
参考

個体間の類似度

$p$ 次元の変数 $\boldsymbol{x}=(x_1,x_2,\cdots,x_p)^\top$ について観察された2個体のデータを

${ \begin{align} A: \boldsymbol{a} &= (a_1,a_2,\cdots,a_p)^\top \\ B: \boldsymbol{b} &= (b_1,b_2,\cdots,b_p)^\top \tag{1} \end{align}}$
とする。個体Aと個体Bの類似度を測る尺度として次のような距離が用いられる。

ユークリッド距離

${\begin{align} d(A,B) = \sqrt{\sum_{i=1}^{p}(a_i - b_i)^2} \tag{2} \end{align}}$

基本的にはこの距離を使う。

基準化ユークリッド距離

${\begin{align} d(A,B) = \sqrt{\sum_{i=1}^{p} \left(\frac{a_i - b_i}{s_i}\right)^2} \tag{3} \end{align}}$

$s_i$ は $x_i$ の標準偏差。

L1距離

${\begin{align} d(A,B) = \sum_{i=1}^{p} |{a_i - b_i}| \tag{4} \end{align}}$

ミンコフスキー距離

${\begin{align} d(A,B) = \left\{ \sum_{i=1}^{p} |{a_i - b_i}|^m \right\}^{1/m} \tag{5} \end{align}}$

$m=1$ のとき $L_1$ 距離、 $m=2$ のときユークリッド距離となる。

マハラノビス距離

${\begin{align} d(A,B) = \sqrt{(\boldsymbol{a}-\boldsymbol{\bar{x}})Σ^{-1}(\boldsymbol{b}-\boldsymbol{\bar{x}})} \tag{6} \end{align}}$

$\boldsymbol{\bar{x}}$ は各変数の平均値が格納されたベクトル、 $Σ^{-1}$ は分散共分散行列。データの標準化を行う場合、すべての共分散が0（分散共分散行列が単位行列）であればマハラノビス距離はユークリッド距離と同じ。

コサイン類似度

コサイン類似度とは、n次元ベクトルの類似性を表す値でありcosθを用いる。距離という尺度を用いず、ベクトル間の方向によって類似性を定義する。ベクトルの向きが一致している場合に1、直交の場合0、向きが逆ならば-1をとる。文書（文字列）や二値データの類似度を比較する際に用いる。

${\begin{align} cos(\boldsymbol{a},\boldsymbol{b}) &= \frac{\boldsymbol{a}・\boldsymbol{b}}{|\boldsymbol{a}||\boldsymbol{b}|} \\ &= \cosθ \tag{7} \end{align}}$

(1)において $p=5$ とし、 $\boldsymbol{a},\boldsymbol{b}$ はそれぞれ以下の値をとるとする。

	$x_1$	$x_2$	$x_3$	$x_4$	$x_5$
$\boldsymbol{a}$	1	1	0	1	1
$\boldsymbol{b}$	1	0	0	0	1

$\boldsymbol{a}$ には1の値が4つ含まれているため $|\boldsymbol{a}|=\sqrt{4}$ 。同様に $|\boldsymbol{b}|=\sqrt{2}$ 。内積は $\boldsymbol{a},[tex:\boldsymbol{b}$ ]が両方1の値をとる変数の数を数えればよいので $\boldsymbol{a}・\boldsymbol{b} = 2$ 。これらを()に代入するとcos類似度は $\frac{2}{\sqrt{4}×\sqrt{2}} = 0.71$ となる。次のデータの場合も同様の計算を行うと、cos類似度は $\frac{1}{\sqrt{3}×\sqrt{3}} = 0.33$ となる。

	$x_1$	$x_2$	$x_3$	$x_4$	$x_5$
$\boldsymbol{a}$	1	1	0	1	0
$\boldsymbol{b}$	1	0	1	0	1

クラスター間の距離

クラスター間（クラスターと各個体間）の距離の定義として代表的なものは、最短距離法*2、最長距離法*3、群平均法、重心法、ウォード法等である。図1に3つのクラスターと最短距離法、最長距離法、重心法における距離のイメージを示す。 $\bar{x_A},\bar{x_B},\bar{x_C}$ は各クラスターの中心（重心）。

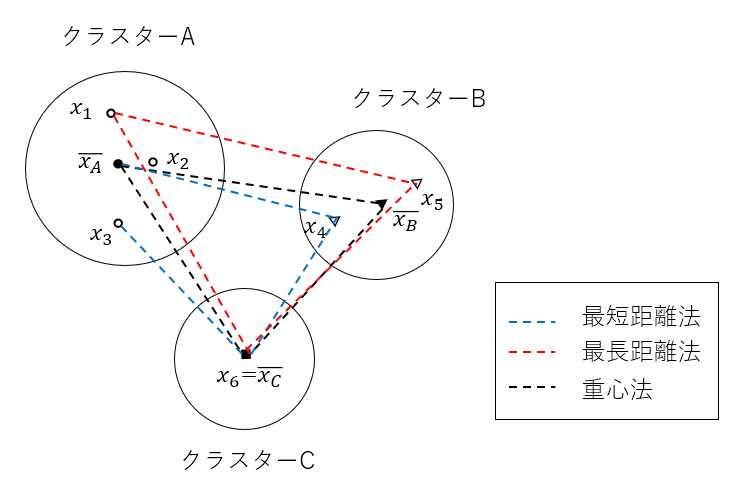
f:id:good_na_life:20210612161725p:plain — 図1

最短距離法は2つのクラスターのそれぞれの中から1個ずつ個体を選び、最も近い個体間の距離とする方法。最長距離法は2つのクラスターの中のそれぞれの中から1個ずつ個体を選び、最も離れた個体間の距離とする方法。群平均法は2つのクラスターに含まれる任意の個体間の距離の平均値を距離とする方法。重心法はクラスターの重心間の距離とする方法。重心法と同様、メディアン法においても重心間の距離を用いるが、融合した（新たに形成した）クラスターの重心の求め方に違いがある。重心法では融合したクラスターの重心をデータ数で重みを付けるのに対し、メディアン法では重心を中点とする。これにはクラスター間で含まれるデータ数に大きな差があるとき、大きいクラスターに引き込まれるのを防ぐ効果がある。

${\begin{align} \text{重心法}：\frac{n_A \bar{x_A} + n_B \bar{x_B} + n_C \bar{x_C}}{n_A + n_B + n_C} \tag{8} \\ \text{メディアン法}：\frac{ \bar{x_A} + \bar{x_B} + \bar{x_C}}{3} \tag{9} \end{align}}$

クラスター間距離として、最短距離法、最長距離法、群平均法を用いる場合は、個体間距離として(2)-(7)すべての距離を用いることができる。しかし重心法、メディアン法、ウォード法を用いる場合、個体間の距離はユークリッド距離に限られる。

クラスターの形成プロセス

クラスタリングの対象とする $p$ 次元 $n$ 個のデータを用意し、データに含まれる個体 $x_i,x_j$ 間の類似度を測る距離 $d_{ij}=d(x_i,x_j)$ を定義する。 $d_{ij}$ を第 $(i,j)$ 成分にもつ $n×n$ の正方行列を $D$ とする。 $D$ は距離行列と呼ばれ、対角成分は0、 $d_{ij}=d_{ji}$ であるため対称行列である。距離行列からもっとも距離が近いデータの組を探し、それらを1つのクラスターにまとめる。ここで得られた最も近い距離は樹形図の1つ目の段差の高さとなり、融合の水準や融合距離と呼ばれる。先ほど形成されたクラスターと残りの個体との距離を定義し、行列数の減った新たな距離行列を作成する。先ほどと同様に最も近い組み合わせ（クラスターと個体間、または個体間）を見つけ、新たなクラスターを形成する。これを繰り返しすべてのデータを1つのクラスターにすれば分析は終了。

例として5人の生徒の数学と英語のテスト結果を用いて、階層型クラスター分析を行う。生徒（個体）間の距離はユークリッド距離、クラスター間の距離は最短距離法を用いる。

f:id:good_na_life:20210613190820p:plain — 表1

個体間の距離行列は図2のようになる。この場合生徒4と生徒5の距離が最も近いため、この組み合わせで新たなクラスターを形成する。生徒4と生徒5の距離1.4は第一ステップにおける樹形図の高さとなる。

f:id:good_na_life:20210613191844p:plain — 表2*4

次に距離が近い生徒1と生徒2を1つのクラスターにまとめ、残りのクラスター（個体）との距離行列を作成する。

f:id:good_na_life:20210613192050p:plain — 表3

生徒1,2と生徒3との距離が最も近いため、ここでさらにクラスターを形成する。最後に生徒1,2,3と生徒4,5のクラスター間の距離が求まり、樹形図が完成する。

f:id:good_na_life:20210613192112p:plain — 表4

f:id:good_na_life:20210613193727p:plain — 図2

図2の樹形図でクラスターの形成過程を確認すると、融合の水準（融合の距離）は1.4、2.0、2.2、2.8と単調に増加している。この性質を融合距離の単調性という。重心法やメディアン法では必ずしもこの性質を有さない。

ウォード法

ウォード法では個体間の距離をユークリッド距離とする。クラスターA、B間の距離（融合の距離）を（A,Bを融合したクラスターの偏差平方和）-{(Aの偏差平方和) + (Bの偏差平方和)}と定義する。ウォード法では起こりうるすべてのクラスターの偏差平方和を調べ、その増加が最小になるようにクラスターを形成する。クラスター形成によって生じる全偏差平方和の増加分が最小になる組み合わせを求める。

f:id:good_na_life:20210612171259p:plain — 図3

図2のクラスターA,B,Cにおける偏差平方和を計算すると、

${\begin{align} W_A &= (x_1 - \bar{x_A})^2 + (x_2 - \bar{x_A})^2 + (x_3 - \bar{x_A})^2 \\ W_B &= (x_4 - \bar{x_B})^2 + (x_5 - \bar{x_B})^2 \\ W_C &= (x_6 - \bar{x_C})^2 = 0 \tag{10} \end{align}}$

このとき全偏差平方和は $W = W_A + W_B + W_C$ *5。クラスターA,Bを融合したとき、平均と偏差平方和は

${\begin{align} \bar{x}_{AB} &= \frac{1}{5}(x_1 + x_2 + x_3 + x_4 + x_5) \\ W_{AB} &= (x_1 - \bar{x}_{AB})^2 + (x_2 - \bar{x}_{AB})^2 + (x_3 - \bar{x}_{AB})^2 \\ &+ (x_4 - \bar{x}_{AB})^2 + (x_5 - \bar{x}_{AB})^2 \tag{11} \end{align}}$