実験計画法（５）2水準の直交表

直交表とは

実験に用いる因子の数が多くなると、水準との組み合わせの数が増え、必要な実験回数が増えてしまう。例えば因子が10個、水準が2つの場合、因子と水準との組み合わせの数は $2^{10}=2014$ となり、少なくとも $1024$ 回の実験が必要になってしまう。企業の製品開発などでは製品の技術的な特性に影響する要因を絞り込めないことが多いため、因子数が多くなることは珍しくはない。そこで、時間や費用の観点からより少ない実験回数で必要な情報が得られる方法について考えられたのが、直交表による実験である。

直交表の使い方

以下は、2水準の場合の直交表（ $L_{8}(2^7)$ ）である。 $L_{8}(2^7)$ の8は行数（実験回数）、2は水準の数、7は列数をそれぞれ表す。直交表の数字1,2は2水準を表す。

直交表は以下の性質をもつ。

1~7列の各列に、数字の1と2が4回ずつ現れる
7つの列のどの2列を取り上げても、数字の並び方は(1,1),(1,2),(2,1),(2,2)の4通りであり、同数回（2回）ずつ現れる

因子間の交互作用がない場合

直交表を用いて、因子が4つ（A,B,C,D）、水準が2個の実験を考える。上表の7列のうち任意の4本の列を因子Ａ,B,C,Dに対応させる（この作業を列に対する因子の割付けと呼ぶ）。ここでは1列：因子Ａ、2列：因子Ｂ、3列：因子Ｃ、4列：因子Ｄとする。ここでは因子の間の交互作用は存在しないと仮定する。直交表の数字1,2を、その列に対応する因子の水準とみなすと、8つの水準組み合わせが決まる。実験No.1ではA1B1C1D1、No.2はA1B1C1D2、となる。この8つの実験をランダムな順番で行い、得られたのが下表の実験データである。

因子間の交互作用がない場合、水準組み合わせをすべて実験せずとも8回の実験データからA,B,C,Dの水準間の比較を行うことができる。各因子の第2水準と第1水準の差は、第2水準の実験データの平均と第1水準の実験データの平均との差をとればよい。因子Aについては、実験No.1~No.4が第1水準、実験No.5~No.8が第2水準なので、対応する実験データの平均の差をとると、(72+73+75+62)/4-(50+43+81+66)/4 = 10.5 となる。つまり第1水準に比べ第2水準の実験データの方が数値が10.5大きくなっている*1。

実験No.1~No.4とNo.5~No.8には因子B,C,Dの2つの水準がそれぞれ同回数（2回）現れる。つまり因子Aの2つの水準には、因子B,C,Dの影響が平等に含まれている。このため、他の因子B,C,Dの影響を制御（コントロール）した状態で、因子Aの水準間の比較を行うことができた。因子間の交互作用が存在しないことを、因子の主効果同士が直交する、という。

因子間の交互作用がある場合

実験によっては因子間に交互作用が発生するものもある。交互作用のある4つの因子を、1列：因子Ａ、2列：因子Ｂ、4列：因子Ｃ、7列：因子Ｄ、と直交表の各列に割付ける。

因子AとBの交互作用は、下表に基づき新たに列を割り当てる*2。

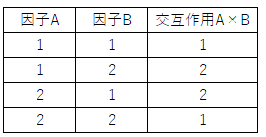
この関係が現れているのが、直交表の3列である。第3列で1をとる実験No1,2,7,8と、2をとる実験No.3,4,5,6の実験データを比較することで、交互作用A×Bの効果を推定することができる。同様に、5列には因子AとCの交互作用A×Cが現れ、実験No1,3,5,8と、2をとる実験No.2,4,6,7を比較すればよい。

この例では3,5,6列に交互作用が現れるが、これらの列に他の因子を割り付けると、この効果が交互作用によるものか、他の因子によるものかが分からなくなる。ある効果と別の効果が分離できなくなる状態を交絡と呼ぶ。

直交表にはあらかじめ成分記号が与えられており、ある2列の成分記号の積をもつ列が、2列の交互作用の現れる列となる。ただし積の計算においては、成分記号の2乗は1となる（ $a^2=b^2=c^2=1$ ）。例えば5列と6列の成分記号は $ac,bc$ であり、この積は $abc^{2} = ab$ 、つまり3列の成分記号と等しくなり、3列に交互作用が現れる。