実験計画法（４）分割法

分散分析、乱塊法に引き続き実験計画法についてのメモ。

分割法の考え方
完全無作為法による1次因子の繰り返し
乱塊法による1次因子の繰り返し
分割法の検定精度
参考文献

分割法の考え方

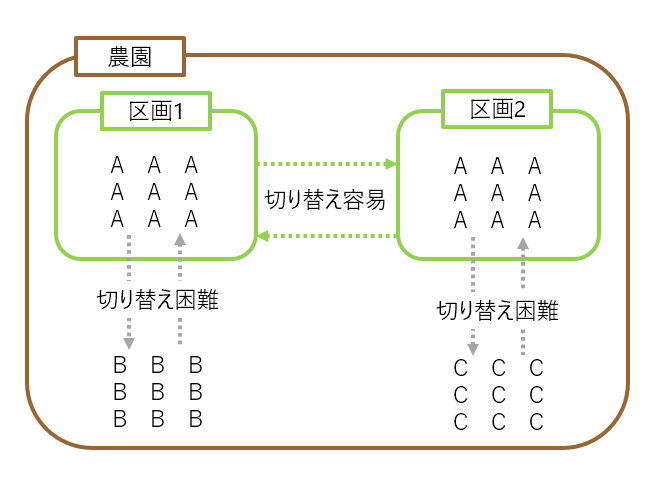
あるコーヒー農園で次のような実験を行う。3つの品種（A,B,C）と2つの区画それぞれでコーヒーを栽培し、コーヒーの収穫量を比較する。3つの品種（A.B,C）を1次因子、と2つの区画を2次因子とする。収穫の数（繰り返しの数）を2回とすると、3品種（1次因子）×2区画（1次因子）×2回繰り返しの合計12回の実験を行うことになる。しかし品種の切り替えには多大な費用と労力がかかるため容易ではない。このような場合、まず品種の実験順序を決め、次に区画の割り当てを決める。実験を容易に行うため、因子の水準の変更回数を少なくするのが分割法の考え方。

分割法では1次誤差と2次誤差の2つの誤差を考える。1次誤差が品種（A,B,C）ごとに生じる誤差、2次誤差が品種（A,B,C）と区画の相互作用によって生じる誤差である。

f:id:good_na_life:20210702060231p:plain — 図1

1次因子の繰り返しの方法には完全無作為法と乱塊法がある。

完全無作為法による1次因子の繰り返し

1次因子（A,B,Cの3つの品種）、2次因子（2つの区画）とし、繰り返し数を2回とする。1次因子（品種）の繰り返しを完全無作為法で行う。この場合1次因子（品種）の切り替え回数は5回で済む。

f:id:good_na_life:20210702061652p:plain — 図2

データの構造式は以下のように表せる。

${ \begin{align} y_{ijk} &= μ + α_i + ε^1_{ik} + β_j + (αβ)_{ij} + ε^2_{ijk} \\ ε^1_{ik} &\sim \mathcal{N}(0,σ^2_1) ,\quad ε^2_{ijk} \sim \mathcal{N}(0,σ^2_1) \tag{1} \end{align} }$

$y_{ijk}$ はコーヒーの収穫量であり、品種 $i = 1,2,3$ 、区画 $j = 1,2$ 、繰り返しの数 $k=1,2$ である。 $ε^1_{ik}$ と $ε^2_{ijk}$ はそれぞれ1次誤差、2次誤差である。このままだと誤差が二つあり計算が困難であるため、反復の効果 $r_k$ を1つの水準と見なし、(1)を繰り返しのない3元配置モデルとして表すことができる。1次誤差 $ε^1_{ik}$ を $α$ と $r$ の交互作用、2次誤差 $ε^2_{ijk}$ を $β$ と $r$ の交互作用だと考えると、(1)は

${ \begin{align} y_{ijk} &= μ + α_i + β_j + (αβ)_{ij} + (αr)_{ik} + (βr)_{ik} + ε_{ijk} \tag{2} \end{align} }$

と表すことができる。

ここでは $ε^1_{ik}= (αr)_{ik}$ 、 $ε^2_{ijk}= (βr)_{ik} + ε_{ijk}$ である。

乱塊法による1次因子の繰り返し

同じく1次因子（A,B,Cの3つの品種）、2次因子（2つの区画）とし、繰り返し数を2回の実験を考える。ここでは1次因子（品種）の繰り返しを乱塊法で行う。

f:id:good_na_life:20210702064138p:plain — 図3

繰り返しの回数 $r_k$ を1つの因子としてデータの構造式に加える。

${ \begin{align} y_{ijk} &= μ + r_k + α_i + ε^1_{ik} + β_j + (αβ)_{ij} + ε^2_{ijk} \\ ε^1_{ik} &\sim \mathcal{N}(0,σ^2_1) ,\quad ε^2_{ijk} \sim \mathcal{N}(0,σ^2_1) \tag{3} \end{align} }$

(1)と同じく繰り返しのない3元配置モデルだと考えると、(3)は

${ \begin{align} y_{ijk} &= μ + α_i +β_j + r_k + (αβ)_{ij} + (αr)_{ik} +(βr)_{jk} + ε_{ijk} \tag{4} \end{align} }$

と表すことができる。ここでは $ε^1_{ik}= r_k + (αr)_{ik}$ 、 $ε^2_{ijk}= (βr)_{jk} + ε_{ijk}$ である。

分割法の検定精度

分散分析の精度は、誤差分散が小さい方がよい。つまり誤差分散の自由度が大きい方がよい。以下のようなデータ構造式を持つ2因子実験の乱塊法の場合、

${ \begin{align} y_{ijk} &= μ + α_i +β_j + r_k + (αβ)_{ij} + ε_{ijk} \tag{5} \end{align} }$

誤差分散の自由度は $(IJ-1)(r-1)$ となる。
他方、分割法において一次因子の繰り返しを乱塊法で行う場合、
一次誤差の自由度は $(I-1)(r-1)$ 、
二次誤差の自由度は $I(J-1)(r-1)$ となる。

いずれにせよ2因子実験の乱塊法における自由度が最も大きい。ただし分割法の場合でも2次誤差の自由度は2因子実験の乱塊法の自由度と同じオーダーであるのに対し、1次誤差の自由度はオーダーが1つ小さい。すなわち1次因子についての検定の精度は悪く、2次因子および1次因子と2次因子の交互作用については検定の精度はよいことが分かる。したがって1次因子の影響はどうでもよく、2次因子および1次因子と2次因子の交互作用について関心がある場合は分割法を用いる。